線占積率とは、四角いコイル断面積に対し、電線が占める割合のことです。
線占積率をWR、コイル断面積がSc、電線断面積がSwとすると
WR=Sw/Sc×100 (%)
と計算します。
この線占積率が分かれば、任意の断面積に何本の電線が巻きつけられるかが分かります。
整列巻きは、2つのパターンがあるので、それぞれについて計算してみましょう。
|
|
| |
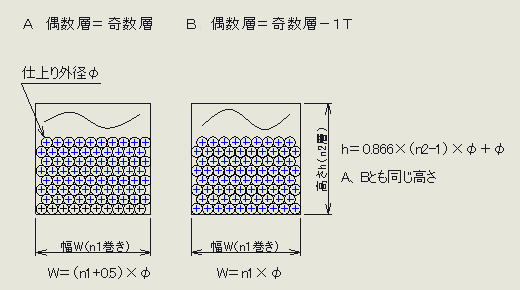
A.
偶数層=奇数層の場合 コイルの断面積 |
|
B.
偶数層=奇数層-1Tの場合 コイルの断面積 |
コイルの幅W=(n1+0.5)*φ
コイルの高さh=0.866×(n2-1)×φ+φ
コイル断面積Sc=W×h
電線の断面積
総巻数N=n1×n2
Sw=π×(φ/2)^2×N
|
  |
コイルの幅W=n1*φ
コイルの高さh=0.866×(n2-1)×φ+φ
コイル断面積Sc=W×h
電線の断面積
総巻数N=n1×奇数層+(n1-1)×偶数層
Sw=π×(φ/2)^2×N
|
例えば、
n1=10T、n2=10層、線径1mmとすると、
W=10.5、h=8.794、Sc=92.337
N=100、Sw=78.53
従って、
WR=78.53/92.337×100 ≒ 85.05 (%)
です。 |
|
例えば、
n1=10T、n2=10層、線径1mmとすると、
W=10、h=8.794、Sc=87.94
N=95、Sw=74.61
従って、
WR=74.61/87.94×100 ≒ 84.84 (%)
です。 |
|
|
|
このように、A、Bともほぼ85%になりました。
任意の四角い断面が分かっている時、その断面積の85%が巻きつけが可能です。
電線の仕上り外径φを決めれば、断面積Scに巻きつけられる本数Nは
Sw=π×(φ/2)^2×N = Sc×0.85
N=Sc×0.85/(π×(φ/2)^2)
となり、計算上で巻線が可能な最大値になります。
ガラ巻の場合は、60~65%で考えています。
|
 |
下表のように巻数を増やすと、90%に近づくようです。
整列巻きと線占積率(偶数層=奇数層)
仕上り外径:1mm
| 1層巻数 |
層数 |
総巻数 |
電線断面積 |
コイル断面積 |
線占積率 |
| n1 |
n2 |
N(T) |
Sw(mm2) |
Sc(mm2) |
WR(%) |
| 5 |
5 |
25 |
19.63 |
24.55 |
79.97 |
| 10 |
10 |
100 |
78.54 |
92.34 |
85.06 |
| 15 |
15 |
225 |
176.71 |
203.42 |
86.87 |
| 20 |
20 |
400 |
314.16 |
357.81 |
87.80 |
| 25 |
25 |
625 |
490.87 |
555.49 |
88.37 |
| 30 |
30 |
900 |
706.86 |
796.48 |
88.75 |
| 35 |
35 |
1225 |
962.11 |
1080.76 |
89.02 |
| 40 |
40 |
1600 |
1256.64 |
1408.35 |
89.23 |
| 50 |
50 |
2500 |
1963.49 |
2193.42 |
89.52 |
| 100 |
100 |
10000 |
7853.98 |
8716.77 |
90.10 |
| 200 |
200 |
40000 |
31415.90 |
34753.47 |
90.40 |
| 500 |
500 |
250000 |
196349.38 |
216783.57 |
90.57 |
| 500 |
1000 |
500000 |
392698.75 |
433500.07 |
90.59 |
|



